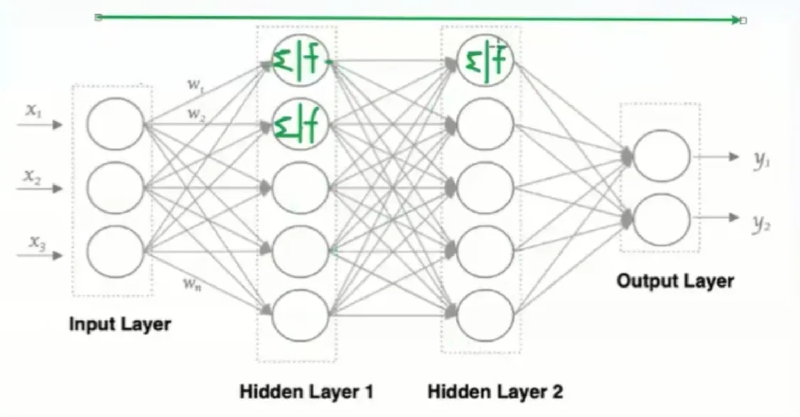
人工神经网络（Artificial Neural Network ，简写：ANN）是模仿生物神经系统（特别是人脑）结构和功能的一种计算模型。它们是深度学习的核心组成部分，赋予了深度学习强大的模式识别和学习能力。

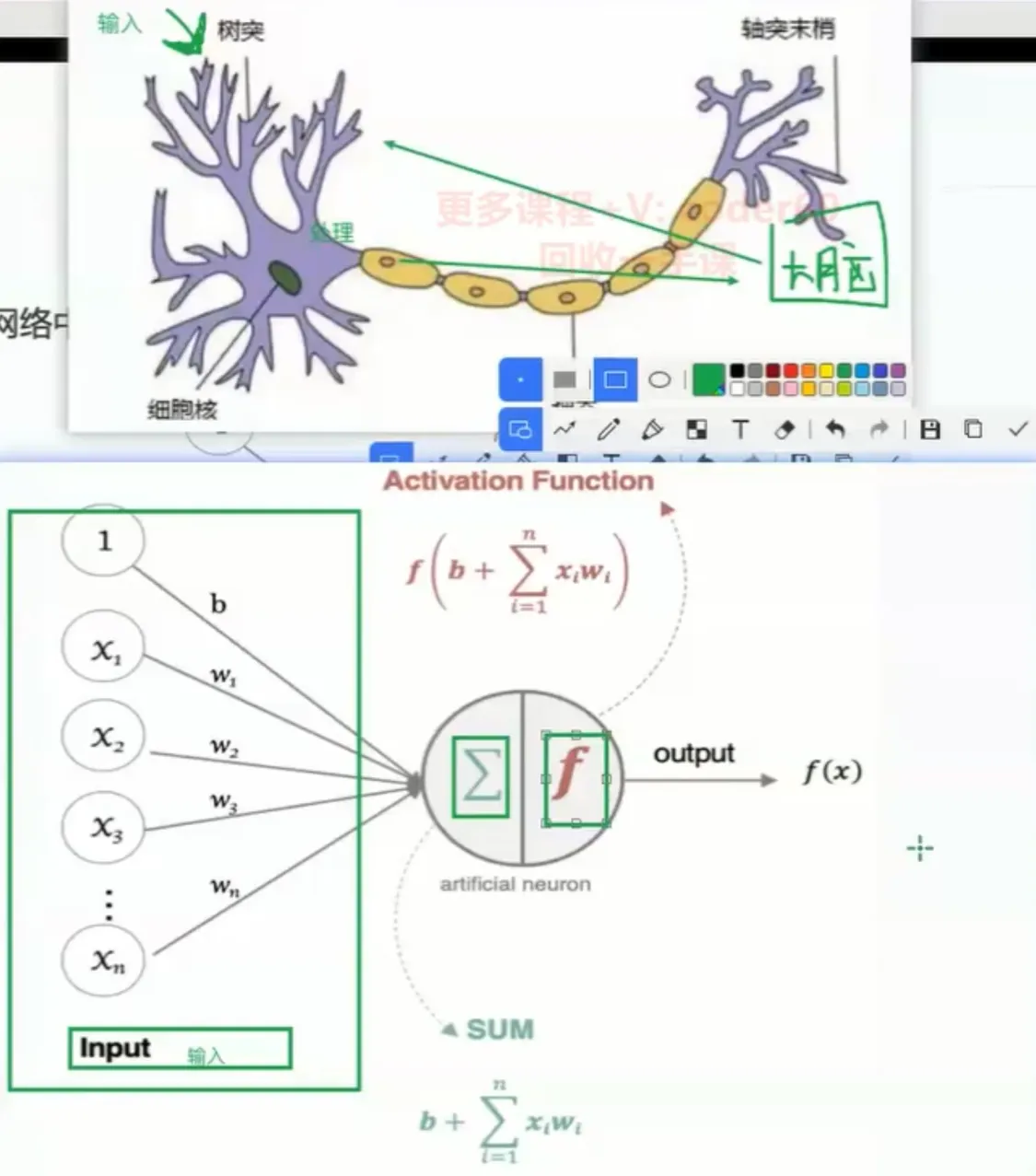
神经网络的基本结构：

一个基本的神经网络由以下几个部分组成：

• 神经元（Neuron）： 也称为节点，是神经网络的基本单元。每个神经元接收输入，进行某种处理，然后产生输出。

• 连接（Connection）： 神经元之间通过连接相互传递信息。每个连接都有一个权重（Weight），表示连接的强度。权重决定了输入信号对输出的影响程度。

• 层（Layer）： 神经元按层组织。一个典型的神经网络包括：

• • 输入层（Input Layer）： 接收外部输入数据。
  • 隐藏层（Hidden Layer）： 位于输入层和输出层之间，负责对输入数据进行处理和转换。深度学习中的“深度”就体现在这里，拥有多个隐藏层。
  • 输出层（Output Layer）： 产生最终的输出结果。

• 特点：

• • 同一层的神经元之间没有连接。
  • 第N层的每个神经元和第N-1层的所有神经元相连（这就是full connection的含义），也称为全连接神经网络。
  • 第N-1层神经元的输出就是第N层神经元的输入。
  • 每个连接都有一个权重值（w系数和b系数）。

神经网络的工作原理：

1. 输入： 输入数据被传递到输入层的神经元。
2. 加权和： 每个神经元接收来自上一层神经元的输入，并将这些输入乘以相应的权重进行加权求和。
3. 激活函数： 将加权和传递给一个激活函数。激活函数引入了非线性，使得神经网络能够学习复杂的模式。常见的激活函数包括Sigmoid、ReLU、Tanh等。
4. 输出： 激活函数的输出成为该神经元的输出，并传递到下一层神经元。
5. 重复： 这个过程在网络中逐层进行，直到到达输出层。

训练神经网络：

训练神经网络的过程包括以下几个步骤：

1. 前向传播（Forward Propagation）：将输入数据通过网络各层传递，计算每个神经元的输出，直到产生最终输出。
2. 损失函数（Loss Function）：计算预测输出和实际标签之间的误差。这种误差称为损失，常见的损失函数有均方误差（MSE）和交叉熵损失（Cross-Entropy Loss）。
3. 反向传播（Backpropagation）：通过损失函数的梯度计算，反向调整每个神经元的权重，以最小化损失。反向传播算法使用链式法则来高效计算梯度。
4. 优化器（Optimizer）：使用优化算法（如梯度下降、Adam 等）根据计算出的梯度更新网络权重，从而减小损失。

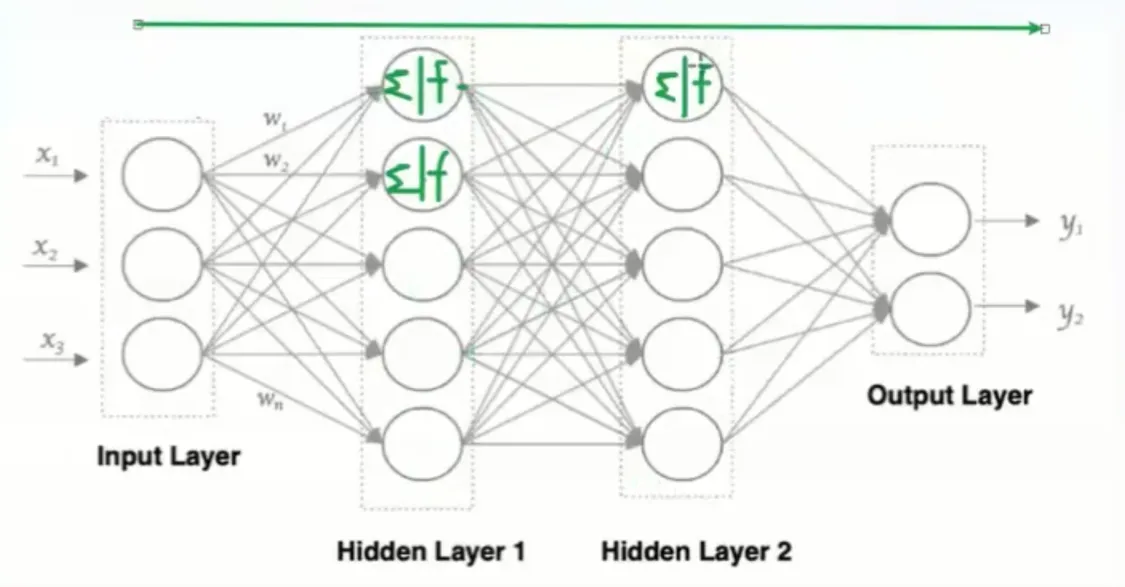
激活函数

加权和在进行输入计算后始终是线性的，需要引入激活函数用于对每层的输出数据进行变换，进而为整个网络注入非线性因素，此时神经网络可以拟合出各种曲线，以此来表达复杂问题的解答。

Pytorch中封装了常见的激活函数

sigmoid 激活函数– 指数型

sigmoid函数一般只用于二分类的输出层

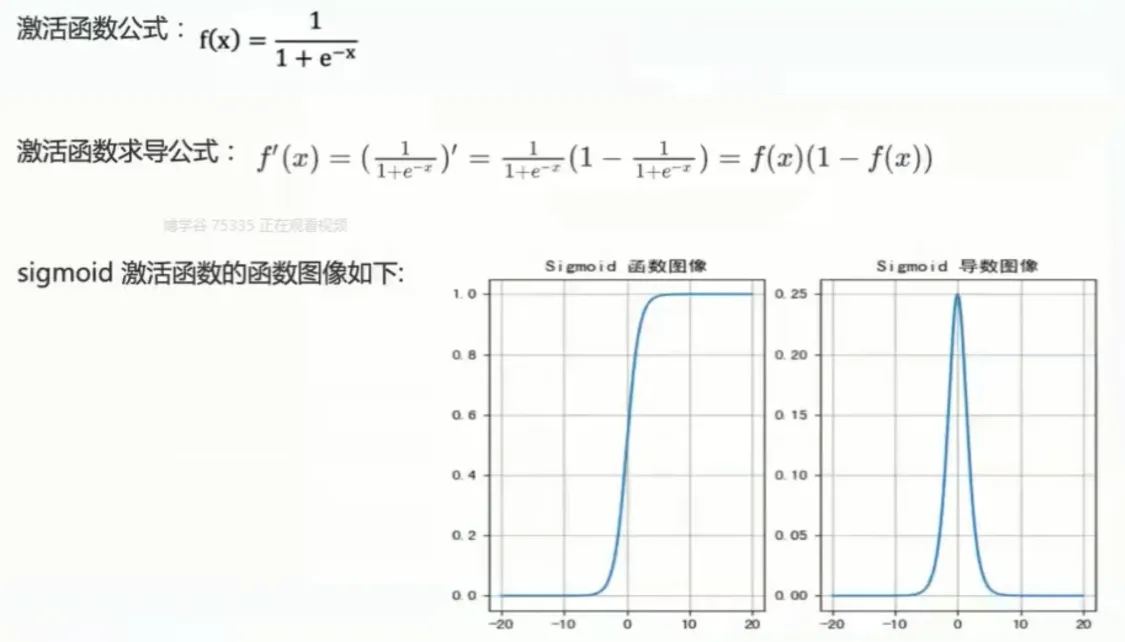
Sigmoid函数，也称为S型函数或乙状函数，是一种形状像字母“S”的数学函数。它在机器学习，特别是深度学习和逻辑回归中，作为激活函数被广泛使用。

定义和公式：

Sigmoid函数最常见的形式是逻辑斯谛函数，其公式如下：

σ(x) = 1 / (1 + e^-x)

其中：

• σ(x) 是函数的输出值。
• x 是函数的输入值（可以是任意实数）。
• e 是自然常数（约等于2.71828）。

图像和特性：

Sigmoid函数的图像呈S形，具有以下特性：

• 定义域： (−∞, +∞) （输入可以是任意实数）
• 值域： (0, 1) （输出值始终在0和1之间，但不包括0和1）
• 单调递增： 输入值越大，输出值也越大。
• 连续光滑： 函数曲线平滑连续，处处可导。
• 在x=0处中心对称： σ(0) = 0.5。
• 导数： σ’(x) = σ(x)(1 - σ(x))，导数可以用函数自身来表示，这在反向传播算法中非常有用。

Sigmoid函数在神经网络中的应用：

在神经网络中，Sigmoid函数通常作为激活函数使用，其主要作用是引入非线性。如果没有激活函数，神经网络就只能进行线性运算，表达能力非常有限。Sigmoid函数将神经元的加权输入转换为0到1之间的输出，可以看作是神经元“激活”的概率。

Sigmoid函数的优缺点：

优点：

• 输出范围有限： 将输出限制在0到1之间，可以方便地表示概率或进行归一化。
• 光滑可导： 方便进行梯度计算，用于反向传播算法。
• 易于理解和使用： 函数形式简单，易于实现。

缺点：

• 梯度消失： 当输入值非常大或非常小时，函数的梯度接近于0。这会导致在反向传播过程中，梯度难以传递到前面的层，从而导致网络训练缓慢甚至停滞。这是Sigmoid函数最大的缺点，也是它在深度神经网络中逐渐被其他激活函数（如ReLU）取代的主要原因。
• 输出不是以0为中心： 输出值始终为正，这可能会导致一些优化问题。
• 计算量较大： 计算指数运算相对耗时。

ReLU激活函数-分段型

ReLu函数常用于隐藏层

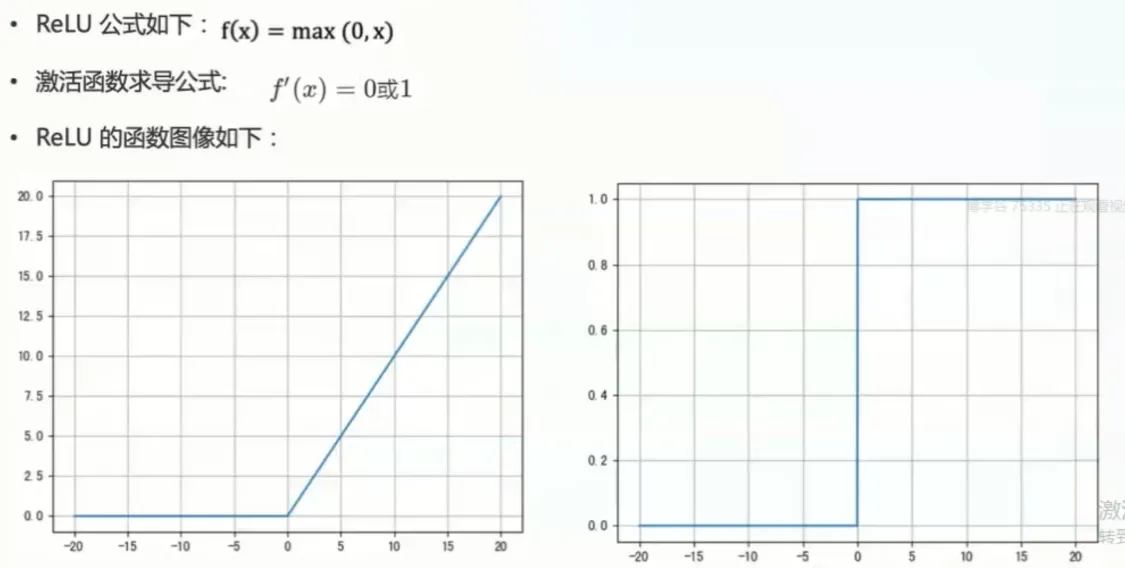
定义和公式：

ReLU函数的数学表达式非常简单：

f(x) = max(0, x)

这意味着：

• 当输入x大于0时，输出等于输入本身（f(x) = x）。
• 当输入x小于等于0时，输出为0。

图像和特性：

ReLU函数的图像由两条直线组成，在x=0处有一个拐点。其主要特性包括：

• 非线性： ReLU函数虽然形式简单，但它是一个非线性函数，这使得神经网络能够学习复杂的模式。
• 计算简单： ReLU函数只需要进行简单的比较和赋值操作，计算速度非常快。
• 单侧抑制： 当输入小于0时，输出恒为0，这导致一部分神经元处于“非激活”状态，有助于网络的稀疏性表达，减少参数之间的相互依赖，缓解过拟合。
• 不存在梯度消失问题（在正区间）： 当输入大于0时，梯度恒为1，这使得梯度可以有效地传递到前面的层，避免了梯度消失问题，加快了网络训练速度。

ReLU函数的优缺点：

优点：

• 缓解梯度消失问题： 这是ReLU最重要的优点之一，它有效地解决了Sigmoid和tanh等激活函数在输入较大或较小时容易出现的梯度消失问题，使得深度神经网络更容易训练。
• 计算速度快： 相比于Sigmoid和tanh等需要进行指数运算的激活函数，ReLU的计算速度非常快，这大大加快了网络的训练速度。
• 促进稀疏性： ReLU的单侧抑制特性使得一部分神经元输出为0，从而产生稀疏的网络结构，有助于减少参数之间的相互依赖，提高模型的泛化能力。

缺点：

• Dead ReLU Problem（神经元死亡问题）： 如果某个神经元的输入在训练过程中一直为负数，那么该神经元的输出将始终为0，导致该神经元“死亡”，不再对网络的学习起到作用。这通常是由于较大的学习率或不合适的初始化参数导致的。

ReLU的变体：

为了解决Dead ReLU Problem，人们提出了一些ReLU的变体，例如：

• Leaky ReLU（带泄漏的ReLU）： 将输入小于0的部分赋予一个很小的斜率，而不是直接设为0。例如，f(x) = x (x>0)；f(x) = αx (x<=0)，其中α是一个很小的常数，例如0.01。这避免了神经元完全“死亡”的情况。
• Parametric ReLU (PReLU，参数化ReLU)： 将Leaky ReLU中的α作为一个可学习的参数，通过反向传播进行学习。
• Exponential Linear Unit (ELU，指数线性单元)： 在输入小于0的部分使用指数函数，而不是简单的线性函数。

ReLU在神经网络中的应用：

ReLU及其变体是目前深度学习中最常用的激活函数之一，尤其在卷积神经网络（CNN）中应用广泛。通常来说，ReLU是隐藏层激活函数的首选。

SoftMax激活函数

常用于处理多分类问题的输出层，将多分类结果以概率的形式展示。

定义和公式：

给定一个包含 n 个实数的向量 z = (z₁, z₂, …, z_n)，Softmax 函数的定义如下：

Softmax(z)_i = e^z_i / Σ_j=1ⁿ e^z_j

其中：

• Softmax(z)_i 表示向量 z 的第 i 个元素的 Softmax 输出。
• e 是自然常数（约等于 2.71828）。
• Σ_j=1ⁿ e^z_j 表示对向量 z 的所有元素的指数求和。

工作原理：

Softmax 函数首先对输入向量的每个元素取指数，然后将每个元素的指数值除以所有元素指数值的总和。这样就保证了输出向量的每个元素都在 (0, 1) 之间，并且所有元素的总和为 1，从而构成了一个概率分布。

Softmax 在神经网络中的应用：

Softmax 函数通常用于神经网络的输出层，尤其是在多分类问题中。例如，在图像分类任务中，神经网络的输出层可以有 10 个神经元，分别对应 10 个不同的类别。经过 Softmax 函数处理后，输出层每个神经元的输出就表示该图像属于对应类别的概率。

Softmax 的优点：

• 输出为概率分布： Softmax 的输出可以直接解释为概率，方便进行分类决策。
• 突出最大值： Softmax 函数能够突出输入向量中值最大的元素，使得分类结果更加明确。

Softmax 的缺点：

• 计算开销： 需要计算指数和求和，计算开销相对较大。
• 梯度消失（在某些情况下）： 当输入向量的某些元素值非常大时，可能会导致梯度消失问题。
• 对输入变化敏感： 输入向量的微小变化可能会导致输出概率的较大变化。

Softmax 与其他激活函数的比较：

• 与 Sigmoid 的比较： Sigmoid 函数通常用于二分类问题，而 Softmax 函数则用于多分类问题。当类别数为 2 时，Softmax 函数退化为 Sigmoid 函数。
• 与 ReLU 的比较： ReLU 函数主要用于隐藏层，而 Softmax 函数主要用于输出层。ReLU 解决了 Sigmoid 的梯度消失问题，但 Softmax 仍然在多分类输出层占有重要地位。

总结：

Softmax 激活函数是一种重要的激活函数，尤其在多分类问题中应用广泛。它将输入向量转换为概率分布，方便进行分类决策。虽然存在一些缺点，但仍然是深度学习中不可或缺的一部分。

补充说明：

• 为了数值稳定性，在实际应用中，通常会对 Softmax 函数的计算进行一些改进，例如减去输入向量的最大值。
• Softmax 函数通常与交叉熵损失函数一起使用，以优化神经网络的训练。

示例：

假设有一个输入向量 z = [2, 1, 0]，则 Softmax 的计算过程如下：

1. 计算每个元素的指数：

• • e² ≈ 7.39
  • e¹ ≈ 2.72
  • e⁰ = 1

1. 计算所有元素指数值的总和：

• • 7.39 + 2.72 + 1 = 11.11

1. 计算每个元素的 Softmax 输出：

• • Softmax(z)₁ = 7.39 / 11.11 ≈ 0.665
  • Softmax(z)₂ = 2.72 / 11.11 ≈ 0.245
  • Softmax(z)₃ = 1 / 11.11 ≈ 0.090

因此，Softmax(z) ≈ [0.665, 0.245, 0.090]。可以看到，这三个数的和接近于 1，并且每个数都在 0 到 1 之间。

激活函数的选择方法 对于隐藏层：

1. 优先选择ReLU激活函数
2. 如果relu效果不好，那么尝试其他激活，如leaky ReLU等。
3. 如果你使用了ReLU,需要注意一下dead ReLU问题，避免出现大的梯度从而导致过多的神经元死亡。

对于输出层：

1. 二分类问题选择sigmoid激活函数
2. 多分类问题选择SoftMax激活函数

其他常见的激活函数

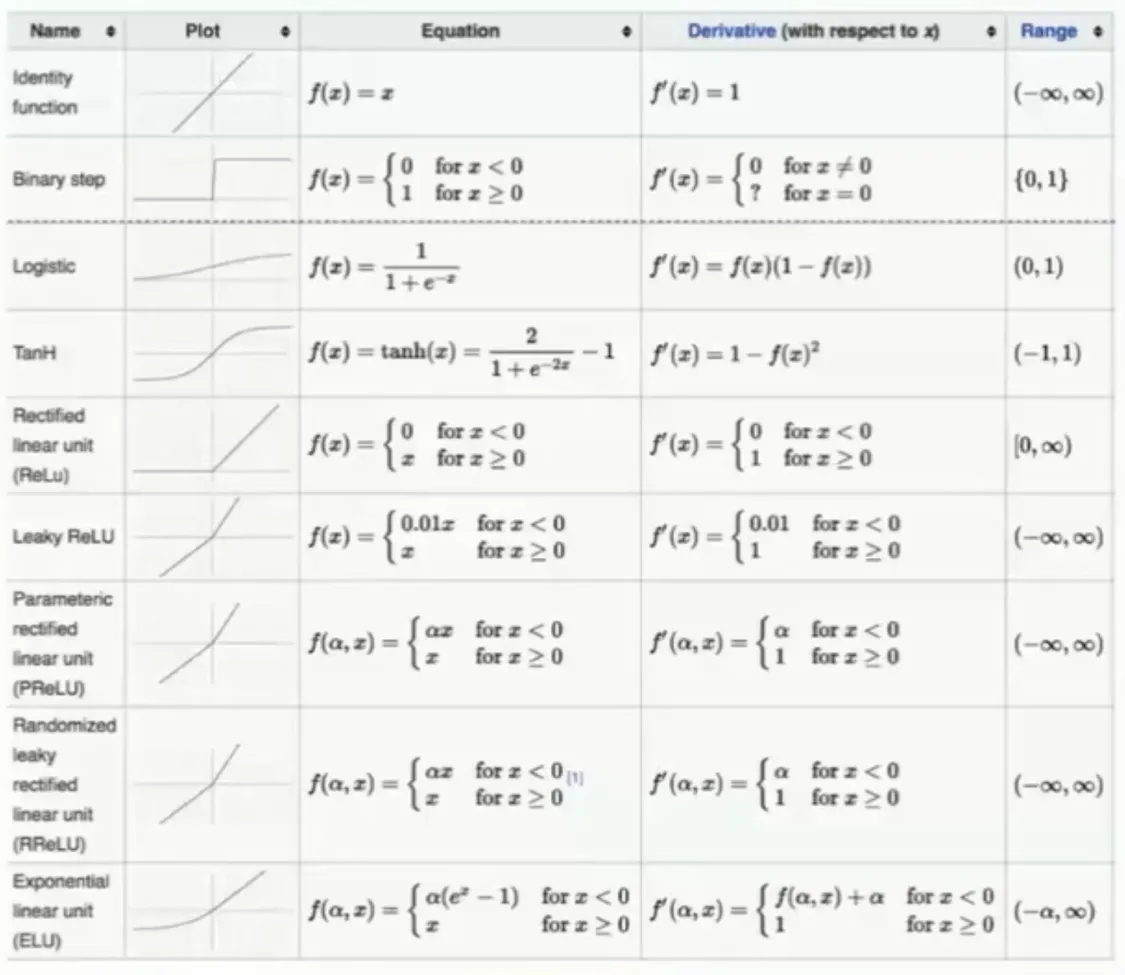
损失函数

什么是损失函数

用来衡量模型参数质量的函数，衡量的方式是比较神经网络输出和真实输出的差异，**损失函数告诉我们模型“犯了多大的错误”。通过最小化损失函数，我们可以优化模型的参数，使其预测结果更接近真实值。**例如：输入一张猫的照片，看输出的结果，

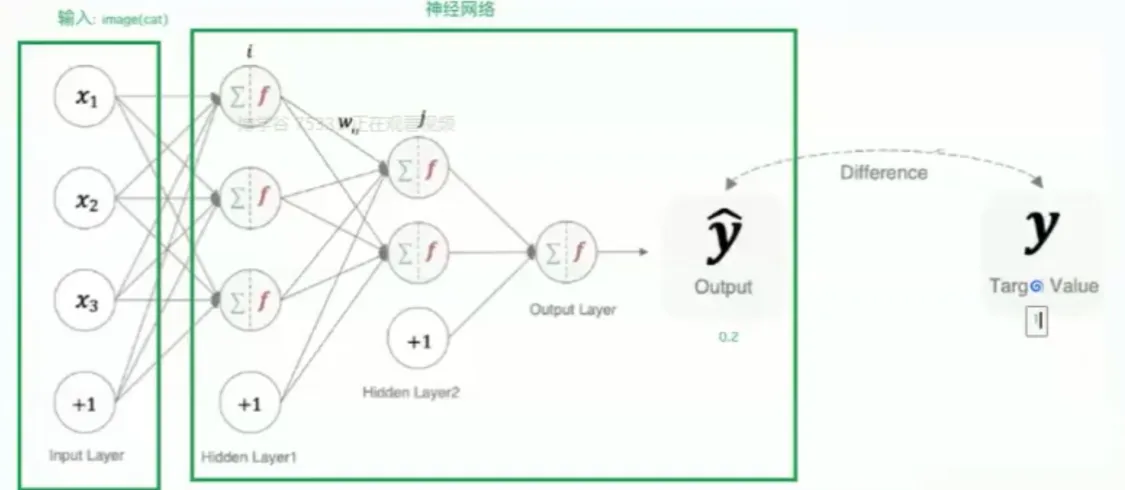
损失函数的作用：

1. 指导模型训练： 在训练过程中，优化算法（如梯度下降）会根据损失函数的梯度来调整模型参数，从而使损失函数的值不断减小。
2. 评估模型性能： 在训练完成后，我们可以使用损失函数来评估模型在测试集上的表现，从而了解模型的泛化能力。

常见的损失函数：

损失函数可以根据任务类型进行分类，主要分为以下两类：

• 回归问题损失函数： 用于预测连续值的任务。
• 分类问题损失函数： 用于预测离散类别的任务。

分类问题损失函数

交叉熵损失（Cross-Entropy Loss）： 常用于多分类问题。

在多分类任务通常使用softmax将logits转换为概率的形式

H(p, q) = - Σp(x)log(q(x))

其中，p(x) 是真实概率分布，q(x) 是预测概率分布。

• 优点： 能够有效地衡量两个概率分布之间的差异，优化效果好。

损失函数与激活函数的关系：

损失函数和激活函数是深度学习模型中两个重要的组成部分，它们之间存在一定的联系。例如，在多分类问题中，通常使用 Softmax 激活函数将输出转换为概率分布，然后使用交叉熵损失函数来衡量预测结果与真实结果之间的差异。

网络优化方法

梯度下降算法是一种用于寻找损失函数最小值的优化算法

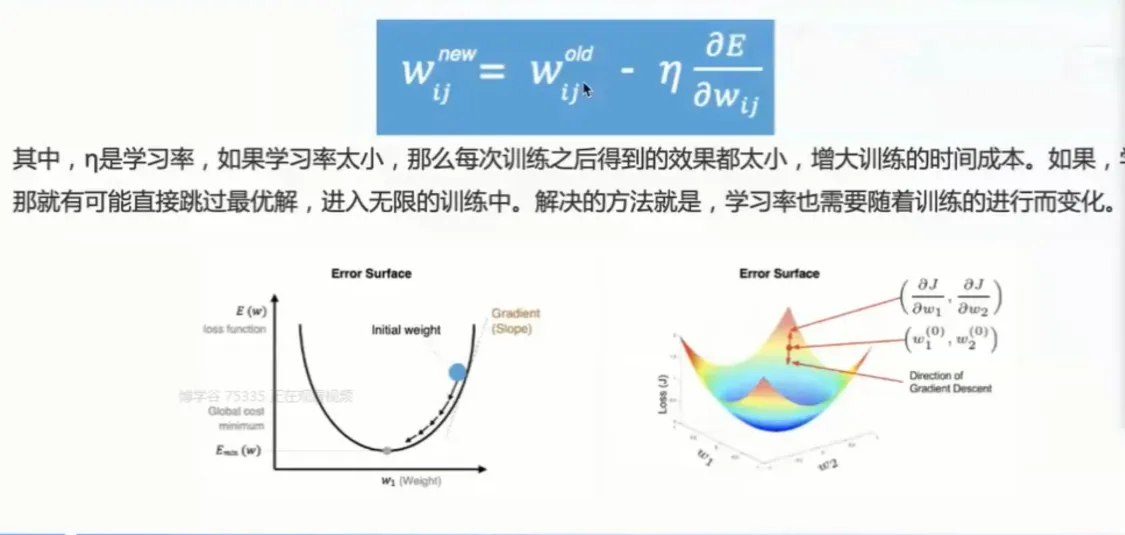
核心思想：

想象你站在一座山上，想要下到山谷。梯度下降法就像你在山上寻找最陡峭的下坡路，然后沿着这个方向走一步，重复这个过程，直到到达山谷的最低点。

数学原理：

• 梯度： 在数学中，梯度是一个向量，它指向函数值增长最快的方向。因此，梯度的反方向就是函数值下降最快的方向。
• 迭代： 梯度下降法通过不断迭代来逼近最小值。每次迭代，它都会沿着梯度的反方向移动一小步。

公式：

θ_new = θ_old - α * ∇J(θ)

其中：

• θ_new：更新后的参数值。
• θ_old：当前的参数值。
• α：学习率（learning rate），控制每次迭代的步长。
• ∇J(θ)：损失函数 J(θ) 关于参数 θ 的梯度。

步骤：

1. 初始化参数： 随机初始化模型的参数 θ。
2. 计算梯度： 计算损失函数 J(θ) 关于参数 θ 的梯度 ∇J(θ)。
3. 更新参数： 使用上述公式更新参数 θ。
4. 重复步骤 2 和 3： 直到损失函数的值收敛到一个可接受的范围内，或者达到预定的迭代次数。

不同类型的梯度下降：

根据每次迭代使用的样本数量，梯度下降法可以分为以下几种类型：

• 批量梯度下降（Batch Gradient Descent, BGD）： 每次迭代使用所有训练样本来计算梯度。

• • 优点： 能够保证收敛到全局最小值（对于凸函数），训练过程相对稳定。
  • 缺点： 计算量大，训练速度慢，不适合处理大规模数据集。

• 随机梯度下降（Stochastic Gradient Descent, SGD）： 每次迭代只使用一个随机选择的训练样本来计算梯度。

• • 优点： 计算速度快，适合处理大规模数据集，有可能跳出局部最小值。
  • 缺点： 训练过程波动较大，不容易收敛到全局最小值。

• 小批量梯度下降（Mini-batch Gradient Descent, MBGD）： 每次迭代使用一小部分随机选择的训练样本（称为一个 mini-batch）来计算梯度。

• • 优点： 结合了 BGD 和 SGD 的优点，既能保证一定的稳定性，又能加快训练速度。
  • 缺点： 需要选择合适的 mini-batch 大小。

学习率的选择：

学习率 α 是梯度下降法中一个重要的超参数，它控制了每次迭代的步长。

• 学习率过大： 可能导致算法在最小值附近震荡，无法收敛。
• 学习率过小： 可能导致收敛速度过慢。

通常需要通过实验来选择合适的学习率。常用的方法包括：

• 试错法： 尝试不同的学习率，观察训练效果。
• 学习率衰减： 随着训练的进行，逐渐减小学习率。

总结：

梯度下降法是一种简单而有效的优化算法，在机器学习和深度学习中有着广泛的应用。理解其基本原理、不同类型以及学习率的选择对于有效地使用梯度下降法至关重要。

补充说明：

除了基本的梯度下降法，还有许多改进的优化算法，例如：

• 动量法（Momentum）： 引入动量来加速收敛，并减少震荡。
• Adam 优化器： 结合了动量法和 RMSProp 的优点，是一种常用的自适应优化算法。

这些改进的优化算法通常能够更快地收敛到最小值，并且对学习率的选择不那么敏感。

前向传播和反向传播

前向传播 传参正向计算的过程

反向传播 参数优化的过程，调整权重参数weight，先从深层开始，逐步到浅层。

前向传播和反向传播视频教程

1
2
3
4
5
6
7
8
9

训练效果由传入的训练量决定，越大越好

假设100000张图片->共15g大小

batch_size 128 表示一次传入的最大参数128张（越大越好）

iter 表示完成一次（128张图片）前向传播和反向传播的**迭代**过程

epoch  表示全部数据（100000张图片）完成一次**轮次**训练